Paper Implementations
Arxiv Link Papers with Code Link

Unless explicitly stated figures belong to the original paper.

Representing 3D World

This is a review for the Point Transformer1 paper which tries to approach point cloud processing tasks with Transformers2.

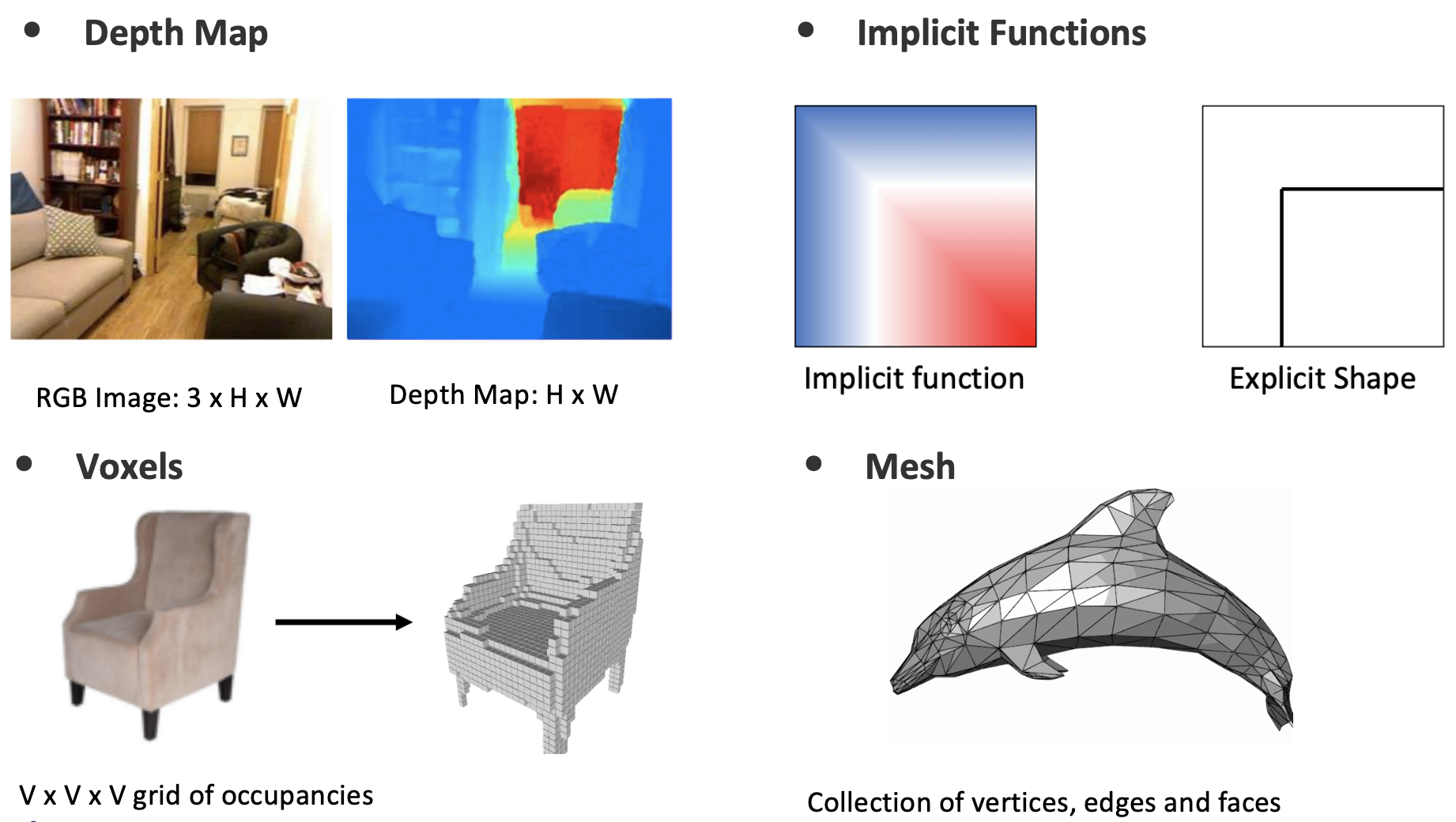
Let’s start with the fundamentals. We can represent the 3D world in multiple ways.

  1. A depth map with an RGB Image
  2. Implicit functions which tells you if a given point is inside the shape.
  3. Volumes to model the objects with voxels
  4. Using meshes to represent objects with vertices, edges, and faces
  5. Point clouds where we have a set of points in space
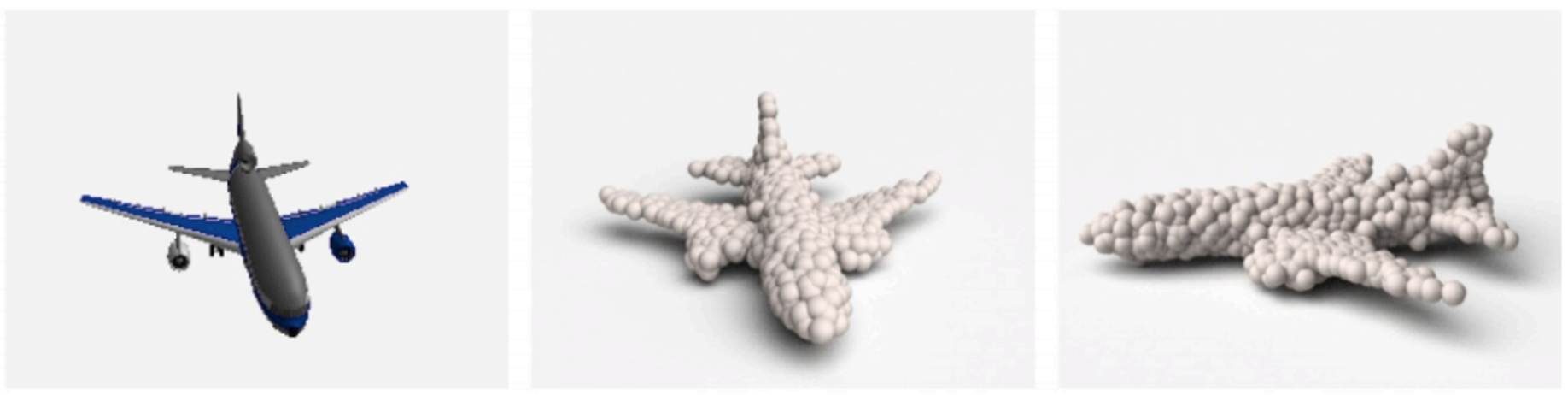
Other representations Point Cloud

Src: Justin Johnson, Michigan University

We are particularly interested in the point clouds in this paper. They represent shapes as a set of data points and we can represent nice shapes with a good amount of points. One downside of point clouds is that we don’t have information about surfaces.

Point clouds have 3 main properties

  1. They are not evenly sampled thus irregular
  2. Each point is individual and neighbors are not at a fixed distance thus unstructured
  3. The order of points does not matter thus unordered

We can approach processing point clouds by projecting to several images and processing them with, for instance, 2D CNNs or by transforming to voxels and processing with 3D CNNs or with similar methods. We can also directly work with point clouds. For example, Pointnet3 directly works with point clouds. Here the important point is we need permutation invariance during the feature extraction. Since the order of points is not important, our processing functions should give the same result if the order of points changes. We achieve this by applying a max pool on the dimension of points which eliminates the importance of the order. Then we can use this global feature vector to gather the output.

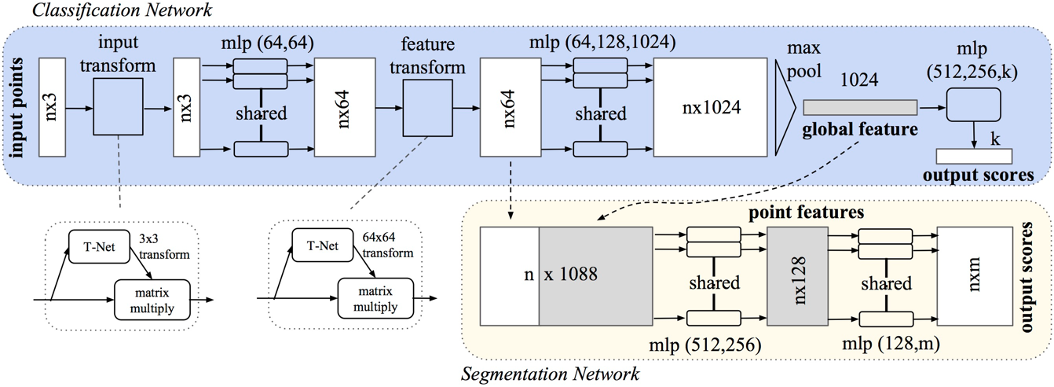
Pointnet Architecture

Attention and Transformers

Transformers are very popular and led to many advancements in NLP in the last years. And now they are being applied in other fields as well. Attention4 is the core idea behind transformers. We try to learn how to focus on important parts while fading out the rest. Generally speaking, we can show 3 types of attention. We will mostly focus on the self-attention.

  1. Soft attention: Attends to input by using learned alignment weights
  2. Hard attention: Attends to predetermined one patch on input
  3. Self*attention: Considers different positions of the same sequence

Self-attention

Most of the explanations of self-attention use the jargon of query, key, and value which can be complicated to understand at first glance. Instead, we will look at the mechanism of attention as matrix multiplications in order to understand the essence of it. Consider the equation below.

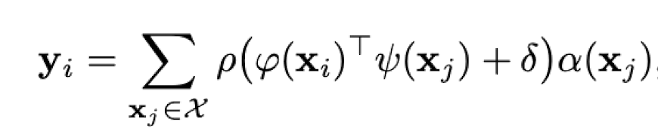
X: 		input feature
Y: 		output feature. 
φ,ψ,α:  pointwise feature transformations, MLP
δ: 		position encoding function 
ρ:		normalization function, softmax.

Here we try to improve our feature vector $X$ and will name it $Y$. For each element $x_i$ of $X$ we loop over all elements of $X$, $x_j$ in this case. We make a pointwise transformation on $x_i$ and $x_j$ with $φ$ and $ψ$, respectively. Afterward dot product of them is calculated. If we want to inject the position information of $x_i$ and $x_j$, we add $δ$. We can roughly call what we have calculated so far as importance factor. Then we multiply this importance factor with the transformed version of $x_j$ with $α$. We normalize our scores with a normalization function $ρ$, softmax in this case. We do this for all $x_j$ and then get the sum of them. By doing this we were able to enhance the information $x_i$ by looking at other portions of the $X$.

In the Transformers paper, attention mechanism is proposed to replace Recurrent Neural Networks for NLP tasks. Attention removes the problem of parallelization and vanishing gradients in RNN. Yet, the memory costly nature of attention made it hard to apply it to more complex data such as vision.

Query, Key and Value

In the paper, for each word we have a query, key, and value. The terminology is that we will give weights to the proposed value of each word by making queries on keys. This terminology comes from the information retrieval field. Consider the example below to see the correspondence between query, key, value and matrix formation of scalar dot product vector attention.

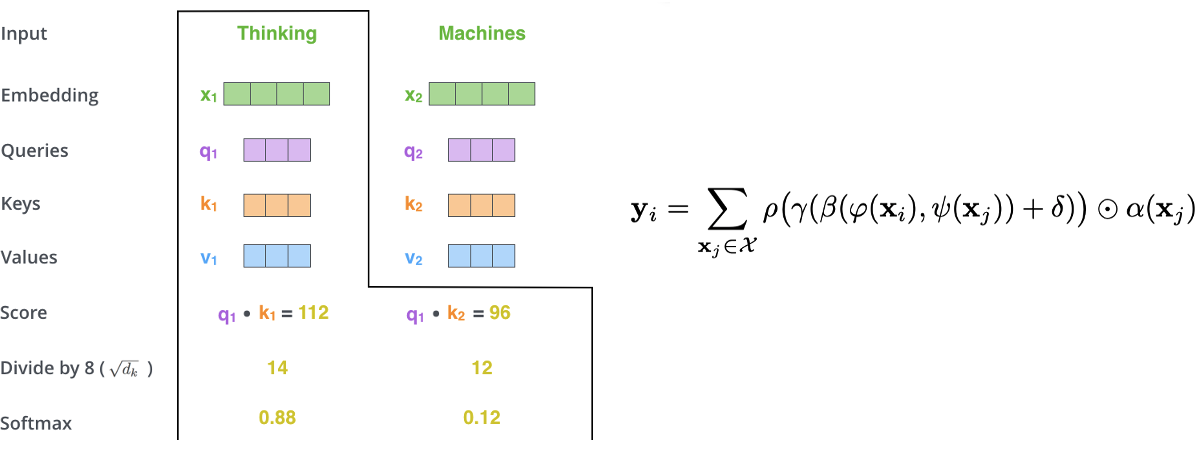corrThe Illustrated Transformer, Jay Alammar

We want to calculate features for the word thinking. But we want to attend in other words in order to have better features. Remember for each word we have query, key, and value. Observe on the left, we calculate the score by getting dot product of query and key for each word in the sentence. We scale it for practical purposes. Then we normalize with softmax. The correspondence is $x_i$ is the query, $x_j$ is the keys. Beta is the relation operation. Here it is the dot product. And ρ is softmax. Very similar.

General Architecture of Transformer

Multi-head attention: Parallel weight matrices. The goal is to expand the model’s ability to focus on different positions

Positional Encoding: It’s a way of injecting information about positions of each input. Consider words in a sentence. The order is important and it changes the meaning. Without a positional encoding, transformer behaves like a bag-of-words system. In the paper, they use sin and cosine functions to encode positions but it’s out of the scope of this review.

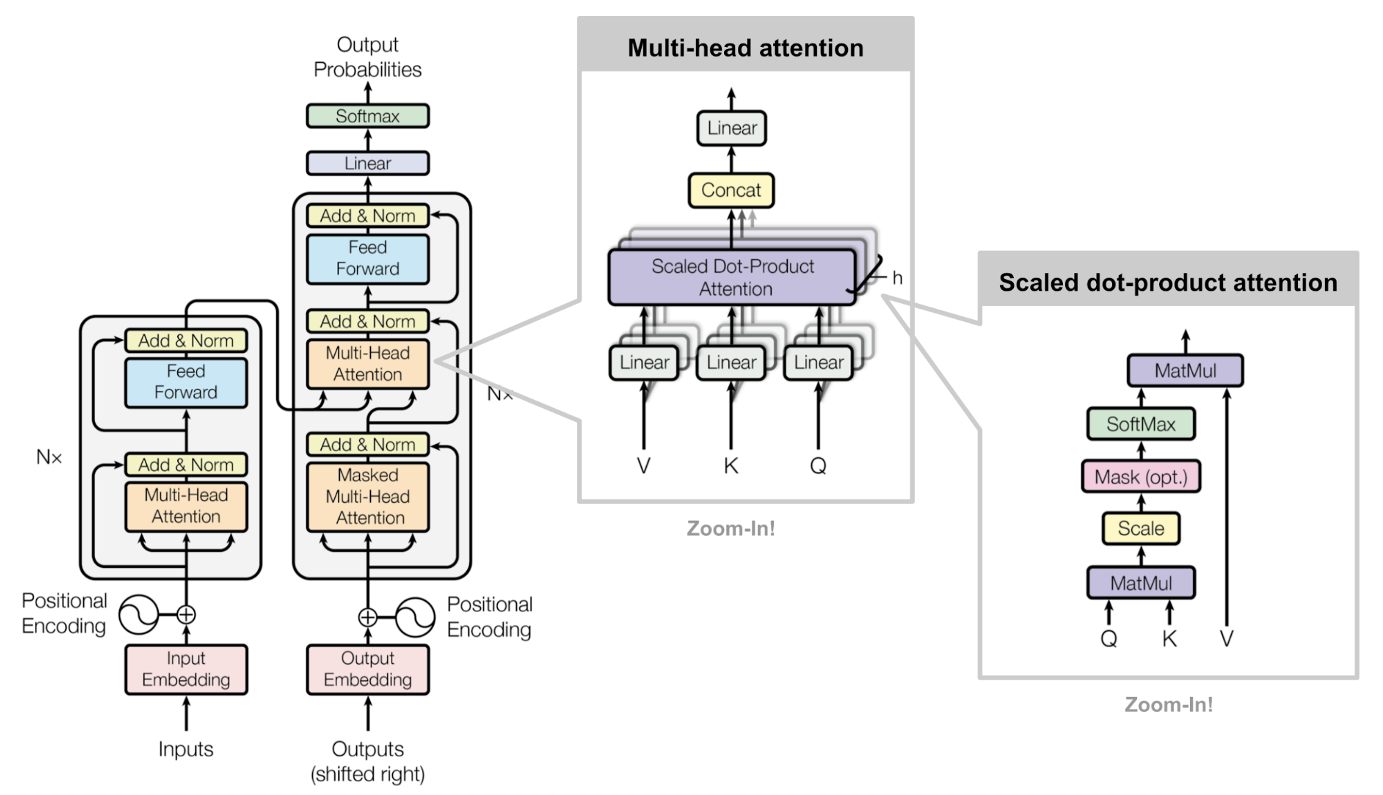corrAttention? Attention!, Lilian Weng

Point Transformer

Motivation

The main motivation of the Point Transformer is the idea that transformers are appropriate for processing point clouds since self-attention is in essence a set operator. Self-attention operation is invariant to permutation and the cardinality of the elements. Which makes it a good candidate for processing point clouds remembering the properties of them.

Main Contribution

  1. A Point Transformer layer
  2. Whole network architecture with Point Transformer layer for tasks like classification and semantic scene segmentation.
  3. State-of-the-art results on several benchmarks.

Method

Point Transformer Layer

The attention equation of our paper has few differences from scalar dot product vector attention. Here the relation operation is subtraction, and they also add positional embeddings here as a result of their ablation study.

Scalar dot product vector attention Attention in Point Transformer

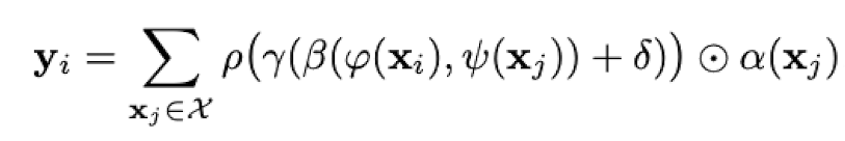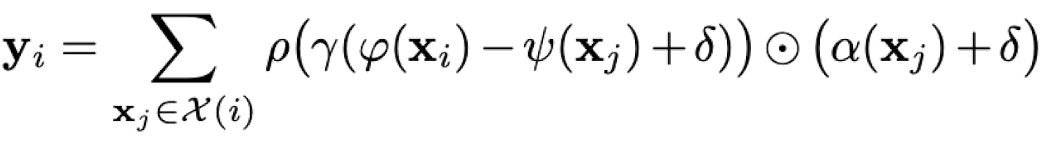Positional Encoding

3D Point coordinates of the points are used for positional encoding as this encodes the position information. It is then transformed with two linear layers and ReLU nonlinearity. Notably, they add positional encoding to both the attention generation branch and the feature transformation branch.

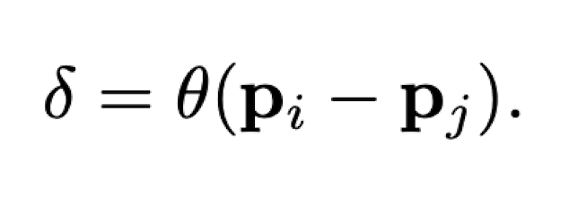
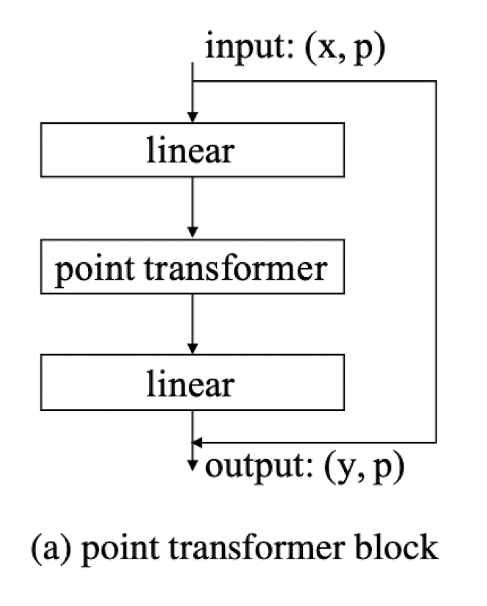
Point Transformer Block

Integrates the self-attention layer, linear projections that can reduce dimensionality, and a residual connection which facilitates information exchange between localized feature vectors.

Transition Layers

They follow U-net approach and have transition down layers in encoder and transition up layer in decoder.

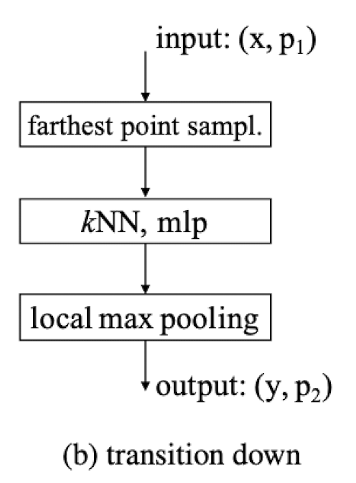
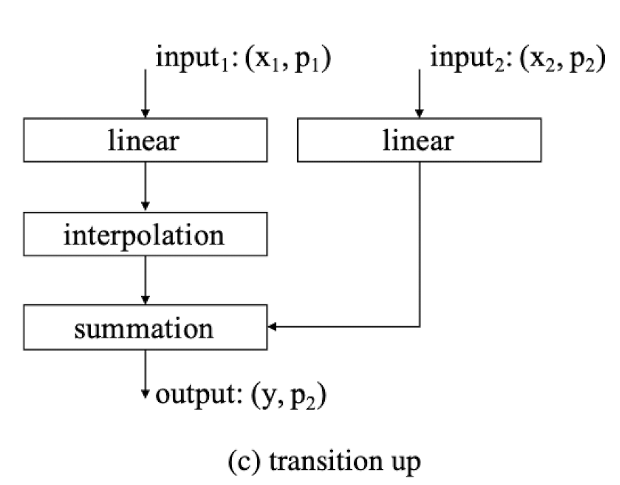
In the transition down layer, cardinality of the point set is reduced. A farthest point sampling in $p1$ conducted to find a subset $p2$ which covers $p1$ well. Then feature vectors are pooled from $p1$ to $p2$ with kNN graph. ($p1$ > $p2$)

For tasks like semantic segmentation which requires dense prediction, transition up layer is also required. Features that are in $p1$ are mapped to $p2$ with trilinear interpolation.($p1$ < $p2$). Features from preceding decoder stage, $x2$, are sent with a skip connection and summarized with the features from the corresponding encoder stage.

Big Picture

Overall architecture can be observed from the figure below. Above is for semantic scene segmentation while below is for object classification.

corr

Experiments

Semantic Scene Segmentation

In semantic segmentation the task is to assign each point to a class of object. For this task they get state of the art results on ShapeNetPart5 dataset.

Quantitative Results Qualitative Results

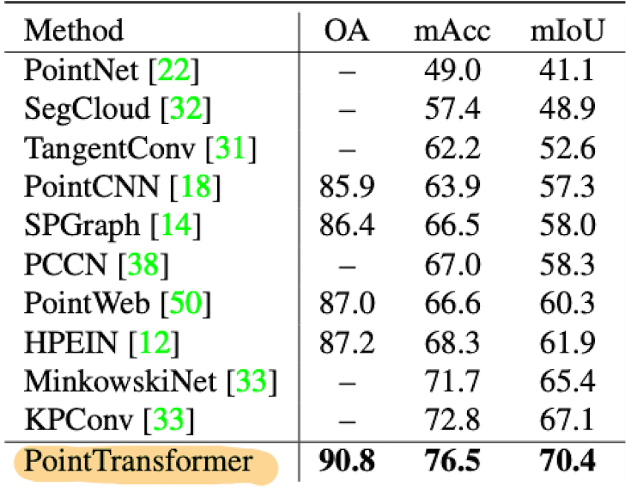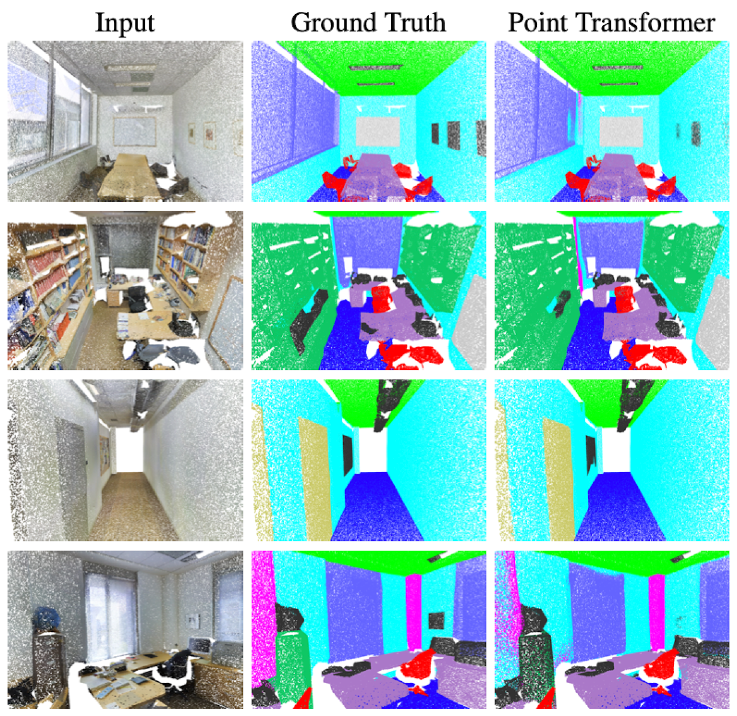Object Part Segmentation

Object part segmentation aims to segment the object to its main parts. They also get pretty good results on ShapeNetPart dataset.

Quantitative Results Qualitative Results

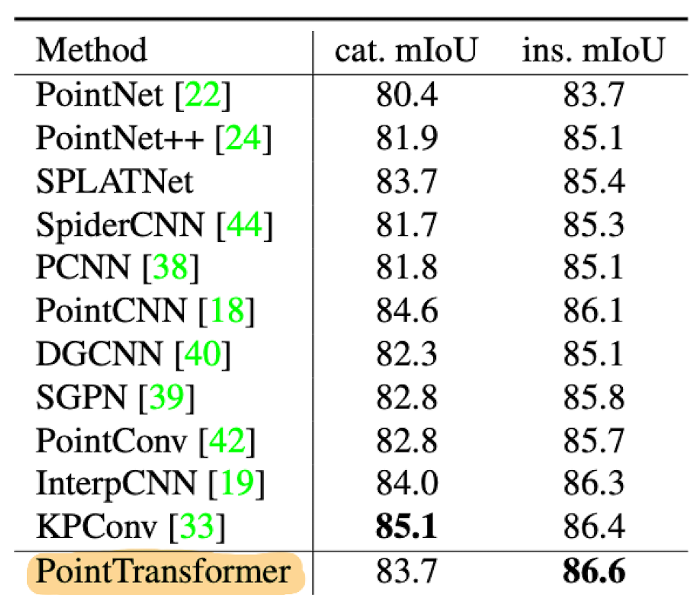Author’s Conclusion

  • Their conceptual idea that point clouds are great fit for transformers turns out to be supported by the experiment results.
  • A performative 3D Scene Understanding Network can be proposed without CNNs or auxiliary branches.
  • Transformers are perhaps an even more natural fit for point cloud processing than language or image processing.

My Opinions

+ Clear explanations of the concepts

+ Great results on classical datasets

+ The model is not complicated yet powerful

- Speed and memory performance of the model is not discussed

- There are not much hints for possible future works or shortcomings of the architecture

- No official implementation is released

- The claim that point cloud processing with transformers should be more natural than language or image processing is not properly discussed.

References

  1. Zhao, H., Jiang, L., Jia, J., Torr, P., & Koltun, V. (2020). Point transformer. arXiv preprint arXiv:2012.09164. ↩

  2. Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., … & Polosukhin, I. (2017). Attention is all you need. arXiv preprint arXiv:1706.03762. ↩

  3. Qi, C. R., Su, H., Mo, K., & Guibas, L. J. (2017). Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition (pp. 652-660). ↩

  4. Bahdanau, D., Cho, K., & Bengio, Y. (2014). Neural machine translation by jointly learning to align and translate. arXiv preprint arXiv:1409.0473. ↩

  5. Chang, A. X., Funkhouser, T., Guibas, L., Hanrahan, P., Huang, Q., Li, Z., … & Yu, F. (2015). Shapenet: An information-rich 3d model repository. arXiv preprint arXiv:1512.03012. ↩